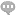测绘相关知识:两点之间的水平直线距离是指在平面上连接两个点的短路径长度。这个概念在地理学、数学和工程学等领域中被广泛应用。距离的计算方法可以根据不同的情况而有所不同。在平面几何中,可以使用勾股定理来计算两点之间的距离。假设有两个点A(x1,y1)和B(x2,y2),它们之间的距离可以通过以下公式计算:距离=√((x2-x1)²+(y2-y1)²)这个公式基于直角三角形的性质,通过计算两个点在x轴和y轴上的坐标差值的平方和的平方根来得到距离。除了平面几何,距离的概念在其他领域中也有不同的应用。在地理学中,距离可以用来衡量两个地点之间的实际物理距离。在数学中,距离可以用来定义度量空间中的距离函数,从而研究空间的性质和结构。在工程学中,距离可以用来评估两个物体之间的相似性或差异性。总之,距离是一个重要的概念,它在各个领域中都有广泛的应用。通过计算两点之间的水平直线距离,我们可以更好地理解和描述事物之间的关系和位置。成都航空摄影测量推荐四川栋量科技有限公司。成都地形图测绘公司哪家好

土方石测量介绍:土方石测量是与工程投资直接相关的重要环节。土石方量的大小对建设工期和经济效益有着直接的影响。因此,准确计算土石方量的精度至关重要。合理的土石方调配可以节省施工费用,并加快工程进度。在计算土石方量时,常用的方法有方格网法、断面法和平均高程法等。在实际应用中,根据工程的具体情况和要求,可以选择合适的土石方量计算方法。通过准确计算土石方量,可以为工程的顺利进行提供重要的参考依据,确保工期和经济效益的实现。成都地形图测绘公司哪家好地形图测绘推荐四川栋量科技有限公司。

大地基准是建立国家大地坐标系统和推算国家大地控制网中各点大地坐标的基本依据。它包括一组大地测量参数和一组起算数据。大地测量参数主要包括地球椭球的四个常数:地球椭球赤道半径、地心引力常数GM、带球谐系数J2(由此导出椭球扁率f)和地球自转角度w。这些参数为建立大地坐系提供了重要的参考。另外,还有一组起算数据用于确定大地坐标系统和大地控制网长度基准。这些数据包括国家大地控制网起算点(也称为大地原点)的大地经度、大地纬度、大地高程以及至相邻点方向的大地方位角。通过大地基准的建立,我们能够准确测量和推算国家各个地点的大地坐标。这对于地理测量、地图制作、导航定位等领域具有重要意义。同时,大地基准也为国家基础设施建设、资源管理和环境保护提供了可靠的空间参考。总之,大地基准是建立国家大地坐标系统和大地控制网的基石,为我们提供了精细的地理信息和空间数据,推动了各个领域的发展和进步。
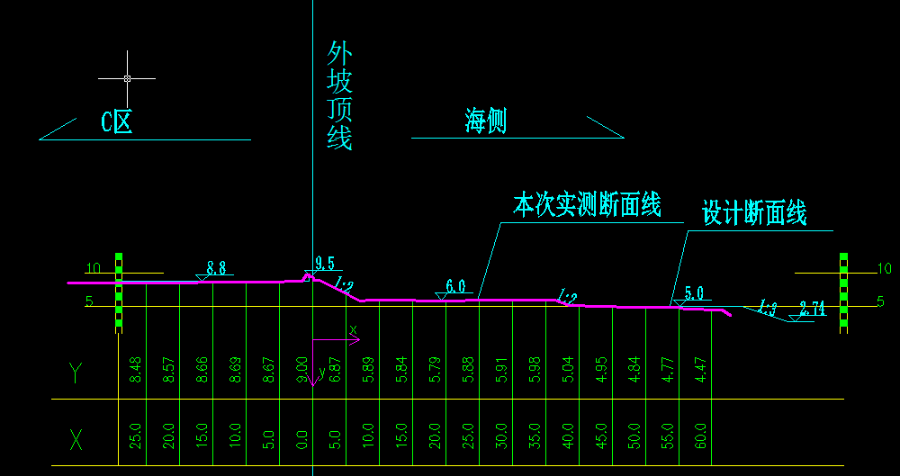
断面测绘是一项用于测量地面起伏的工作,它主要针对某一方向的剖面进行测量。这项工作通常分为纵断面测量和横断面测量。纵断面测量是指对线路中线桩地面高程进行测量,其具体施测方法与一般水准测量相同,也被称为路线水准测量。通过纵断面测量的成果,我们可以绘制出纵断面图,这些图可以供设计坡度时使用。横断面测量则是对线路的横向剖面进行测量,主要是为了了解线路在横向上的地形变化情况。通过横断面测量,我们可以获得线路在不同位置的地面高程数据,从而更好地了解线路的地形特征。四川测绘推荐四川栋量科技有限公司。

测绘在科学研究和教育中也具有重要的应用价值。科学家可以利用测绘技术对地球表面进行详细的测量和绘制,研究地球的地貌、地质、气候等特征,深入了解地球的演化和变化规律。同时,测绘还可以为教育提供丰富的教学资源,通过地图和地理信息系统,帮助学生更好地理解地理知识,培养他们的地理思维和空间认知能力。综上所述,测绘在国土资源管理、城市规划和建设、科学研究和教育等方面都具有重要的意义和广泛的应用。随着科技的不断发展,测绘技术也在不断创新和进步,为人类社会的发展和进步做出了重要贡献。成都土方石测量推荐四川栋量科技有限公司。成都管线测量一般多少钱
四川形变监测推荐四川栋量科技有限公司。成都地形图测绘公司哪家好
断面测绘介绍:断面测绘是一项用于测量地面起伏的工作,它主要针对某一方向的剖面进行测量。这项工作通常分为纵断面测量和横断面测量。断面测绘在工程建设中起着重要的作用。通过对地面起伏的测量,我们可以更准确地了解地形情况,为工程设计提供重要的参考依据。同时,断面测绘也可以帮助我们评估工程建设对地形的影响,从而采取相应的措施进行调整和优化。断面测绘是一项重要的测量工作,它可以帮助我们更好地了解地形起伏情况,为工程建设提供准确的数据支持。通过纵断面测量和横断面测量,我们可以获得详细的地形数据,为工程设计和规划提供有力的支持。成都地形图测绘公司哪家好
文章来源地址: http://swfw.chanpin818.com/jiancefuwu/deta_23517906.html
免责声明: 本页面所展现的信息及其他相关推荐信息,均来源于其对应的用户,本网对此不承担任何保证责任。如涉及作品内容、 版权和其他问题,请及时与本网联系,我们将核实后进行删除,本网站对此声明具有最终解释权。



 [VIP第1年] 指数:3
[VIP第1年] 指数:3